Współczesne techniki wytwarzania, szczególnie te wykorzystujące obrabiarki CNC, w zakresie doboru parametrów technologicznych bazują na oprogramowaniu CAM, często współpracującym z programami CAD
Skuteczność inżynierskich programów CAM zależy w znacznym stopniu od poprawności modelu rodzaju obróbki (np. frezowanie w obróbce skrawaniem) oraz modelu obrabiarki (np. pionowe centrum obróbkowe czy konwencjonalna obrabiarka do obwiedniowej obróbki kół zębatych). Dobór parametrów obróbki może zależeć od współczynników opisujących i weryfikujących efekt końcowy obróbki lub jej pojedynczego etapu (np. ślad współpracy międzyzębnej). Poprawność algorytmu i dokładność obliczeń modelu stanowi podstawowe zagadnienie, jakie należy rozwiązać podczas opracowywania lub doskonalenia oprogramowania CAM.
Model stanowi ?układ założeń przyjmowanych w danej nauce przy rozpatrywaniu pewnego problemu w celu uproszczenia lub umożliwienia jego rozwiązania?, a także ?zależność opisująca wyidealizowane zjawisko fizyczne lub ekonomiczne, przyrząd do rozwiązania takiej zależności; interpretacja różnych pojęć i teorii matematycznych? [SJP1]. W pracach [RM1, KA1, ST1] założono idealnie sztywny, bezbłędny geometrycznie i kinematycznie model, w którym nie występują zjawiska takie jak: zużycie, odkształcenie cieplne.
W takim ujęciu każdy model zawsze będzie jedynie ograniczonym opisem rzeczywistości i nigdy jej nie zastąpi. Z tego powodu stopień uszczegółowienia obliczeń i przybliżeń wyników odgrywa niebagatelne znaczenie.
W programowaniu i sterowaniu procesem obróbki, np. na pionowym centrum frezarskim, wykorzystuje się komputerowe układy sterowania. Przygotowanie technologiczne nie ogranicza się do doboru parametrów obróbki, ale umożliwia także wybranie właściwej ścieżki przebiegu ruchu roboczego narzędzia. Zagadnienie to odgrywa ważną rolę w obróbkach wysokowydajnych.
W dalszej części artykułu przedstawiony jest, na bazie obwiedniowej obróbki stożkowych kół zębatych o linii zębów koło-łukowej wg metody Gleason Helixform, przykład budowy obliczeń i algorytmu syntezy powierzchni bocznej zęba (PBZ) tzw. koła dużego (napędzanego), obrabianego metodą kształtową [RM1]. W przypadku tej obróbki dobór parametrów obróbkowych został przeprowadzony dla obrabiarki konwencjonalnej, uzależniony jest przede wszystkim od poprawności przebiegu śladu współpracy międzyzębnej kół przekładni. Do analizy współpracy międzyzębnej konieczne jest wyznaczenie PBZ obu kół przekładni.
W tym oraz innych przypadkach zastosowanie CAM ma na celu skrócenie czasu potrzebnego na technologiczne przygotowanie produkcji i obniżenie kosztów poprzez zredukowanie do niezbędnego minimum stosowania doświadczalnej metody doboru parametrów obróbkowych.
Obecnie konwencjonalne obrabiarki do obróbki obwiedniowej kół zębatych zastępowane są przez nowoczesne obrabiarki CNC (6-osiowe). Ze względu jednak na koszty obrabiarki konwencjonalne są w dalszym ciągu w użyciu, często nawet pomimo kilkudziesięciu lat użytkowania. Dlatego opracowywanie modeli na potrzeby oprogramowania CAM znajduje zastosowanie również w przypadku maszyn technologicznych niesterowanych numerycznie lub co najwyżej zmodernizowanych do poziomu NC.
Artykuł prezentuje, na wybranym fragmencie opisu metody Gleason Helixform, syntezę modelu [RM1], nie zaś oprogramowania CAM, co jest czynnością przeznaczoną dla zespołu informatyków programistów.
W syntezie modelu obróbki [RM1] wykorzystano przede wszystkim zasady obliczeń opracowane przez [KA1] dla charakterystycznego punktu P, który położony jest na PBZ w połowie szerokości wieńca, na stożku podziałowym. W ten sposób definiowane jest podstawowe położenie punktu P. W celu uzyskania poprawnej współpracy międzyzębnej możliwa jest relokacja punktu P.
Powierzchnia działania narzędzia
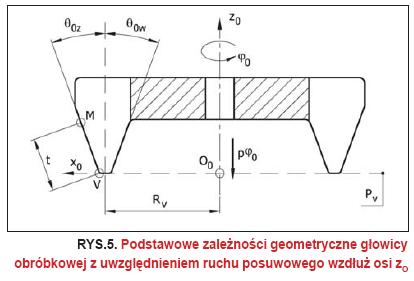
Powierzchnia działania narzędzia (głowicy frezowej) stanowi pobocznicę stożka o półkącie wierzchołkowym równym kątowi zarysu noża.
Założono, że noże zewnętrzne głowicy narzędziowej obrabiają część wklęsłą zęba zębnika, napędzającą część wypukłą koła współpracującego, co znajduje odbicie w dalszej części przy wyprowadzaniu równań wektorów normalnych. Równanie tej powierzchni może być rozpatrywane jako równanie prostoliniowego zarysu krawędzi skrawającej ze stopniem swobody ?0, czyli obrotem głowicy wokół własnej osi. Równanie z uwzględnieniem posuwowego ruchu głowicy w układzie xOyOzO przyjmuje następującą postać:
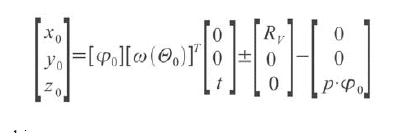
gdzie:
?0 ? ogólne oznaczenie kąta zarysu noża,
RV ? ogólne oznaczenie promienia wierzchołków głowicy
RV = RVW ? dla noży wewnętrznych,
RV = RVZ ? dla noży zewnętrznych.
t ? parametr równania, który rozumiany jest jako odległość od wierzchołka V do rozpatrywanego punktu M krawędzi skrawającej.
Kąt ?0 może przyjmować następujące wartości:
- przy rozpatrywaniu zarysu noża dla ujemnych współrzędnych x0:
?0 = ?0w > 0 ? dla krawędzi wewnętrznej,
?0 = ?0z < 0 ? dla krawędzi zewnętrznej,
przy czym obowiązuje znak ??? przed wektorem zawierającym RV.
- przy czym obowiązuje znak ??? przed wektorem zawierającym RV.
?0 = ?0w < 0 ? dla krawędzi wewnętrznej,
?0 = ?0z > 0 ? dla krawędzi zewnętrznej,
przy czym obowiązuje znak ?+? przed wektorem zawierającym RV.
- p ? współczynnik opisujący dodatkowy ruch posuwowy głowicy obróbkowej wzdłuż osi zO w funkcji kąta obrotu ?0 wokół osi zO, wartość wyznaczono w [RM1]:
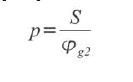
Gdzie S stanowi długość skoku głowicy opisaną równaniem
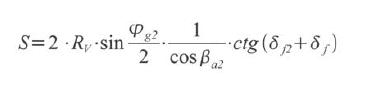
Prawdziwość tego równania zachowana jest wyłącznie przy spełnieniu określonych warunków. Głowica frezowa obrabiająca koło talerzowego wykonuje 10 skoków, każdy na pełną głębokość. Wymaga to uwzględnienia przedziału kątowego obrotowego ruchu głowicy, w którym realizowany jest jeden pełny skok na jeden nóż głowicy.
Wyznaczanie powierzchni bocznej Ak2
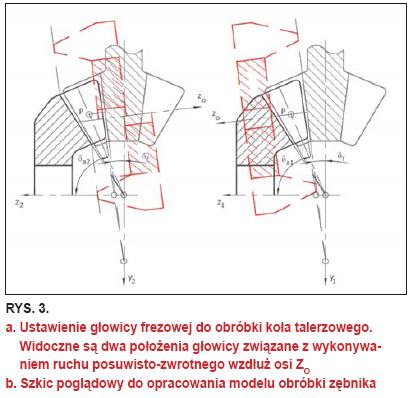
Wyznaczanie równania PBZ koła talerzowego (dużego) Ak2 (rys. 3, 6) według technologii jego wytwarzania. W metodzie Gleason Helixform ząb koła obrabiany jest poprzez kształtowe wcinanie się dwustronnego narzędzia z dodatkowym ruchem posuwowym wzdłuż osi głowicy, co jest wymuszone przez równoległe ustawienie osi głowicy obróbkowej koła dużego względem osi głowicy narzędziowej do obróbki zęba zębnika.
Wyznaczenie omawianego równania składa się z następujących etapów:
1. Pozycja wyjściowa
2. Obrót względem osi x2 o kąt 270°-?f2. Płaszczyzna czołowa głowicy PV pokryje się z tworzącą stożka stóp obrabianego koła talerzowego.
3. Przesunięcie głowicy wzdłuż osi yo (1) do punktu P
4. Obrót głowicy obróbkowej wokół osi xo (2) w celu ustawienia osi głowicy równolegle względem osi głowicy przeznaczonej do obróbki zębnika
5. Obrót wokół osi zo (3) o wartość pochylenia linii zęba ßa2 obrabianego koła na stożku stóp zębnika
7. Przesunięcie głowicy o promień ustawczy Rouk. Przed Rouk obowiązuje znak ?+? dla prawej linii zęba oraz znak ?-? dla lewej linii zęba
8. Równanie powierzchni działania narzędzia w układzie: xo (5) yO (5) zO (5) można zapisać następująco:
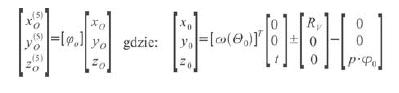
9. Ruchy ustawcze polegające na obrocie wokół osi zo (kąt ?u2) oraz przesunięciu wzdłuż tej samej osi (hz2) wynikającym z ruchu posuwowego. W omawianym modelu kształtowania przyjęto, że obrót ustawczy realizowany jest między położeniem punktu obliczeniowego względem punktu charakterystycznego P a położeniem wyjściowym pracy głowicy. Przyjęto, że wartość kąta obrotu ustawczego równa jest połowie zakresu kątowego potrzebnego na wykonanie przez narzędzie jednego pełnego skoku na jeden nóż (tu 18°).
Równanie opisujące PBZ Ak2 przyjmuje ostateczną postać:
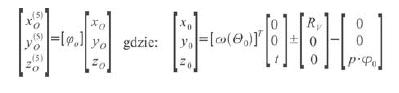
ze zmiennymi: t i ?0.
W celu przeprowadzenia analizy przebiegu śladu współpracy międzyzębnej należy oprócz powierzchni Ak2 wyznaczyć równania opisujące powierzchnie:
- wyobrażalnego koła narzędziowego Ak1,
- PBZ zębnika Am
- PBZ zębnika At, zwaną również powierzchnią odniesienia ? to powierzchnia, która wchodzi w przypór z PBZ zęba koła współpracującego całą swoją powierzchnią i służy do analizy modyfikacji PBZ zębnika (Am),
- stożków określających obszary, w których istnieją powierzchnie, pozwalające na odrzucenie punktów spełniających warunki generowania lecz znajdujących się poza obszarem.
Znajomość PBZ Ak2 i Ak1 pozwala na wyznaczenie równań opisujących odpowiednio powierzchnie Am i At [KA1, RM1, ST1].
W omawianym modelu powierzchnie opisywane są w sposób dyskretny (punktami), w efekcie określona PBZ jest przedstawiona w postaci ?chmury? punktów. Na etapie konfiguracji obliczeń można określić gęstość ? liczbę punktów dla danej powierzchni. W [RM1] przyjęto, że około 500 punktów opisuje PBZ i ta liczba wystarcza na potrzeby zastosowań przemysłowych. Deklarowana pośrednio liczba punktów wpływa znacząco na czas obliczeń, które w przypadku powierzchni złożonych z kilkudziesięciu tysięcy punktów mogły trwać nawet kilka godzin.
Po wyznaczeniu powierzchni w postaci dyskretnej, sparametryzowaniu powierzchni Ak2 [KD1] można było przystąpić do analizy współpracy międzyzębnej, przeprowadzanej z zastosowaniem specjalistycznego programu komputerowego [KD1]
Podsumowanie
Model zbudowany jest na założeniach, które umożliwiają rozwiązanie problemu, lecz jednocześnie stanowią pierwsze ograniczenie dokładności obliczeń. Obecnie analiza współpracy mechanicznej poddawana jest również badaniom wytrzymałościowym (metoda elementów skończonych – MES), które stanowią uzupełnienie modelu obróbki.
Doświadczenie wzbogaca wiedzę i umożliwia doskonalenie algorytmów i samych obliczeń, poprawiając skuteczność oprogramowania CAM.
Z praktycznego punktu widzenia nie powinno się traktować oprogramowania CAM jako swoistej wyroczni w zakresie technologicznego przygotowania produkcji. Zadaniem CAM jest skrócenie czasu tego procesu poprzez zmniejszenie kosztownych próbnych obróbek. W rzeczywistości produkcyjnej zdarza się, że program obróbki musi być korygowany ze względu na odmienne luzy poszczególnych obrabiarek tego samego modelu podczas produkcji tego samego elementu. Oprogramowanie CAM nigdy nie zastąpi ani operatorów, ani technologów, gdyż nie jest możliwe kompleksowe uwzględnienie wszystkich czynników wpływających na obróbkę.
Przedstawiony skrótowo przebieg syntezy modelu obróbki PBZ koła talerzowego z przekładni hipoidalnej ukazuje fragmentarycznie złożoność problemu generowania modeli obróbki.