Elementarz modelowania powierzchniowego (cz. VI)

Kontynuując rozważania na temat opisu matematycznego elementów geometrycznych w systemach CAD trzeba jeszcze dodać, że model matematyczny powierzchni jest rozszerzeniem modelu matematycznego krzywej

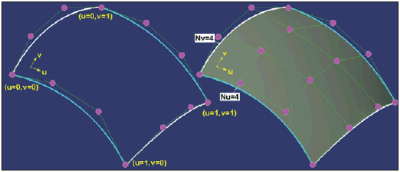
RYS. 1.

Przestrzeń parametryczna takiego modelu zostaje rozszerzona z jednowymiarowej (u) w przypadku krzywych do dwuwymiarowej (u, v) w przypadku powierzchni. I tak, jeśli mamy 4 krzywe Béziera stopnia d°=3 (4 punkty kontrolne), zamykające pewien obszar w przestrzeni 3D (Rys. 1), to powierzchnia Béziera „rozpięta” na tych krzywych jest opisana siecią 4 x 4 = 16 punktów kontrolnych.

Jeśli jedna z krzywych podstawowych powierzchni jest typu NUPBS lub NURBS, to powierzchnia wynikowa też jest typu NUPBS lub NURBS. Stopień powierzchni w każdym z jej kierunków głównych (u lub v) jest oczywiście taki, jak stopień jej krzywych podstawowych w tych kierunkach, a modyfikacje dowolnego punktu kontrolnego sieci powodują – podobnie jak w przypadku krzywych – stosowne zmiany kształtu powierzchni: globalne w przypadku powierzchni Béziera i lokalne w przypadku powierzchni typu NUPBS lub NURBS. Ponadto, podobnie jak dla krzywych, obowiązują te same zasady dotyczące zachowania warunków ciągłości pomiędzy definiowanymi powierzchniami. Nie zamierzam jednak rozwijać tego tematu, uznając, że jest bardzo intuicyjny, zwłaszcza po szczegółowym wyjaśnieniu tego zagadnienia w zakresie krzywych.

Po takiej, mam nadzieję nie za dużej dawce teorii powróćmy do konstruktora mechanika, który ma za zadanie zdefiniowanie modelu powierzchniowego jakiejś części. Napisałem mechanika, aby ograniczyć zestaw funkcji CAD do takich, których używa mechanik, a nie stylista (patrz „Sztuka modelowania powierzchniowego w systemach CAD”, Design News, Wrzesień 2006). Załóżmy, że tenże konstruktor ma już zdefiniowane dwie powierzchnie (A i B na Rys. 2), a jego zadaniem jest zdefiniowanie kolejnej powierzchni C łączącej A z B.

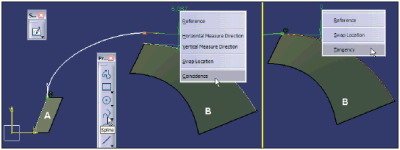
RYS. 2.

Mechanik rozpoczyna definiowanie powierzchni od definicji krzywych. Tu może zastosować szereg różnych funkcji, z których najprostsze wydaje się zdefiniowanie konturu (środowisko Sketcher w systemie CATIA V5). Jeśli kształt definiowanej powierzchni, a dokładniej krzywa przekroju przez tą powierzchnię nie jest trywialnym przypadkiem krzywej drugiego stopnia (łuk okręgu, wycinek elipsy lub paraboli), to taka krzywa może być zdefiniowana poleceniem Spline (Rys. 2). Oczywiście, skoro trzeba „dopasować” tą krzywą do wcześniej zdefiniowanych powierzchni A i B, to należy zdefiniować zgodność (Coincidence) jej punktów końcowych z krzywymi przekrojów powierzchni A i B (ciągłość typu G0) oraz jeśli w modelu końcowym nie powinno byś ostrej krawędzi, to także styczność (Tangency) do tych przekrojów (ciągłość typu G1). Rodzaj oraz liczba krzywych, jakie trzeba przygotować przed rozpoczęciem definicji powierzchni zależy od rodzaju funkcji, którą konstruktor zamierza zastosować. Zanim jednak przejdę do definicji powierzchni chciałbym przypomnieć, że jakość powierzchni końcowej zależy od jakości krzywych zastosowanych do jej definicji.

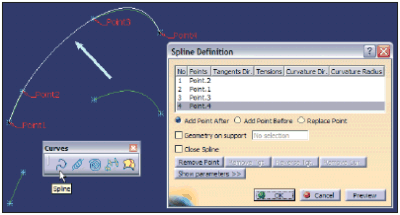
Dlatego, mimo że mechanika na ogół nie interesuje matematyczny model krzywej, a jedynie spełnienie wymagań konstrukcyjnych (zgodność punktów skrajnych, styczność, ciągłość itp.), to powróćmy na chwilę do teorii i postawmy pytanie: jakiego typu krzywą jest Spline zdefiniowana w środowisku Sketcher?. Definicja takiej krzywej polega na wskazaniu kolejnych punktów (1,2,3,4 na Rys. 3), przez które system prowadzi krzywą gładką. Jeśli przekształcimy tą krzywą w krzywą swobodną (na przykład poleceniem Control Points środowiska FreeStyle), to system zdefiniuje krzywą opisaną wielobokiem 12 punktów kontrolnych, złożoną z 3 segmentów, z których każdy jest opisany przez 6 punktów kontrolnych. Czyli jest to krzywa typu B-Spline zbudowana z 3 krzywych Béziera stopnia d°=5 połączonych ze sobą z zachowaniem ciągłości typu G2. Dokładniej należałoby powiedzieć, że jest to krzywa wielomianowa (Polynomial) z nierównomiernym (Non- Uniform) rozkładem węzłów (NUPBS). W środowisku Sketcher konstruktor nie widzi wieloboku punktów kontrolnych krzywej typu Spline i w związku z tym nie może modyfikować położenia punktów kontrolnych, ale może zmieniać położenie (współrzędne na płaszczyźnie szkicu) punktów węzłowych tej krzywej. Nie ma też możliwości modyfikacji rozkładu węzłów, czyli zmiany sposobu parametryzacji krzywej, ale w środowisku FreeStyle może uprościć opis krzywej redukując stopień krzywych cząstkowych na przykład do d°=3. Takie uproszczenie modelu matematycznego generuje oczywiście nową krzywą, która różni się nieznacznie (tu o 0,228 mm) od krzywej pierwotnej. Warto myślę przypomnieć, że to konstruktor podejmuje decyzję, która z krzywych spełnia wymagania konstrukcyjne i nawet, jeśli krzywa B-Spline stopnia d°=3 różni się od krzywej stopnia d°=5, to nie jest to jednoznaczne z odrzuceniem tej krzywej.

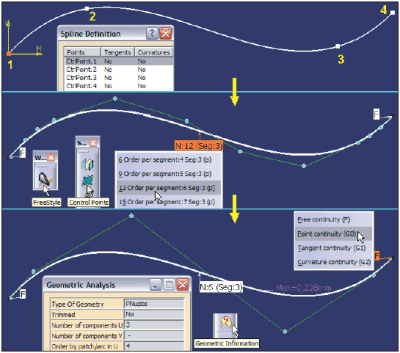
RYS. 3.

Jeśli zdefiniowane zostały wszystkie wymagane krzywe, to można przystąpić do definicji powierzchni. Tu mechanik ma do wyboru kilka metod:

• Powierzchnia typu LOFT (polecenie Multi-sections Surface), która gwarantuje ciągłość typu G0 lub G1 wzdłuż krawędzi wspólnych z powierzchniami A i B (Rys. 4), a kształt powierzchni może być określony przez dowolną liczbę jej przekrojów – stąd multi-sections w nazwie. Krzywe przekrojów muszą być płaskie i ponadto, jeśli konstruktor wskazuje własną krzywą Spine w definicji tego typu powierzchni, to płaszczyzny, na których leżą te krzywe muszą być prostopadłe do krzywej.
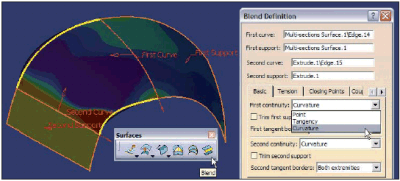
• Powierzchnia typu BLEND (polecenie Blend), która umożliwia zdefiniowanie powierzchni z ograniczonymi możliwościami kontroli kształtu powierzchni w kierunku poprzecznym do krawędzi wspólnych z powierzchniami A i B, ale za to możliwością wyboru rodzaju ciągłości (G0, G1 lub G2) wzdłuż krawędzi wspólnych. Graniczne krzywe „przejścia” z powierzchni A na B różnią się od zdefiniowanych wcześniej przekrojów (zaznaczone kolorem żółtym na Rys. 5), ale powierzchnia wynikowa ma wyższy stopień ciągłości z powierzchniami sąsiednimi.
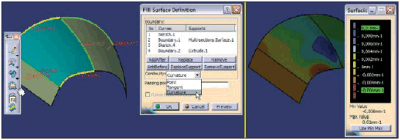
• Powierzchnia typu FILL (polecenie Fill), która gwarantuje ciągłość typu G0, G1 lub G2 wzdłuż wszystkich krawędzi powierzchni C, a więc także krawędzi wspólnych z powierzchniami A i B (Rys. 6), ale praktycznie bez kontroli kształtu „wnętrza” powierzchni.

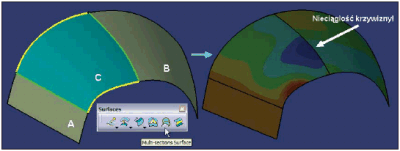
RYS. 4.

RYS. 5. 

RYS. 6.

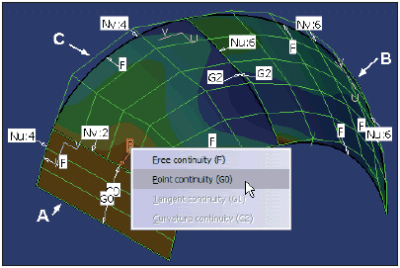
Rezultat zastosowania każdej z tych funkcji – czyli powierzchnia C – spełnia nie tylko różne warunki ciągłości z powierzchniami A i B, ma różny kształt, ale także różny rozkład zmian krzywizny. Jeśli mechanik buduje model powierzchniowy i wymagana jest ciągłość typu G2, a żaden z powyższych sposobów nie spełnia wymagań konstruktora, to musi on zmienić metodę. Na przykład jeśli wyjdziemy z założenia, że pojedyncza krzywa lub powierzchnia ma zawsze ciągłość typu G2 (de facto standard w większości systemów CAD), to zamiast definiowania trzech powierzchni (A, B i C) i trzech zestawów krzywych można rozważyć definicję jednego „globalnego” zestawu krzywych, a potem… jednej powierzchni.

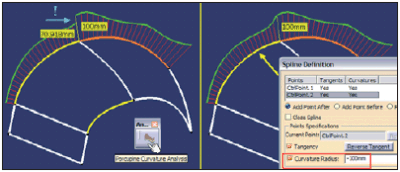
Kilka krzywych, które mają być ze sobą połączone z zachowaniem ciągłości G2 muszą mieć znany przebieg zmian krzywizny. Szczególnie ważne są wartości promienia krzywizny w punktach skrajnych tych krzywych. Na przykład, jeśli dwie krzywe pokazane na Rys. 7 mają w punkcie wspólnym promienie krzywizny równe odpowiednio 70,918 mm i 100 mm to, aby zapewnić warunek ciągłości G2 pomiędzy tymi krzywymi można zmodyfikować pierwszą z nich, czyli tą, która została zdefiniowana jako Spline w środowisku Sketcher. Ustalenie warunku styczności oraz promienia krzywizny w punkcie CtrlPoint.2 tej krzywej rozwiązuje problem ciągłości. 

RYS. 7.

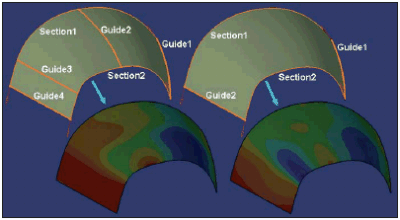
Podobną procedurę trzeba powtórzyć dla każdego innego punktu, w którym jest wymagane zachowanie ciągłości G2 krzywych. W kolejnych krokach należy połączyć odpowiednie krzywe (polecenie Join) i zdefiniować powierzchnię, na przykład Multi-sections Surface (Rys. 8). Liczba krzywych, na których „rozpinana” jest powierzchnia powinna być starannie przemyślana – bo nie jest prawdą, że im więcej krzywych, tym lepsza powierzchnia wynikowa. Dotyczy to oczywiście nie tylko krzywych przekrojowych (Sections), ale także krzywych prowadzących (Guides).

RYS. 8.

Rozkład zmian krzywizny jest lepszy niż poprzednio, choć niekoniecznie na tyle dobry, aby usatysfakcjonować wymagającego konstruktora. Zamiast modyfikacji pojedynczych krzywych i łączenia ich w krzywe zespolone (Join) można zastosować inną metodę. Definicja każdej krzywej opiera się zazwyczaj na ustaleniu kilku punktów, przez które krzywa musi być poprowadzona. Zwykle jest to punkt początkowy i końcowy oraz kilka punktów pośrednich. Jeśli zdefiniujemy takie punkty skrajne dla krzywych przekrojowych powierzchni A i B (Rys. 9), to na bazie tych punktów można zbudować krzywą typu Spline (polecenie Spline środowiska Wireframe and Surface lub Generative Shape Design). W obszarach pomiędzy punktami Point1 i Point2 oraz Point3 i Point4 tak zdefiniowana krzywa będzie oczywiście różna od pierwotnie zdefiniowanych krzywych przekrojów (kolor zielony na Rys. 9), ale z pewnością będzie ona miała ciągłość G2, a charakter zmian krzywizny będzie bardziej jednorodny. Zadaniem konstruktora jest ocena, czy taka krzywa spełnia wymagania konstrukcyjne i może być zastosowana w definicji powierzchni.

RYS. 9.

Jeśli żadna z wyżej opisanych metod nie gwarantuje pozytywnego rezultatu, to trzeba zastosować funkcje z zakresu modelowania powierzchni swobodnych (FreeStyle) – mechanik musi skorzystać z funkcji, które na ogół stosuje stylista. Algorytmy modelowania swobodnego umożliwiają definiowanie i modyfikacje krzywych oraz powierzchni w oparciu o ich modele matematyczne. Precyzyjnie należałoby powiedzieć, że konstruktorstylista definiuje kształt krzywej lub powierzchni dostosowując położenie jej punktów kontrolnych. Może to robić „na piechotę” przez ustalenie warunków ciągłości powierzchni wzdłuż wszystkich jej krzywych granicznych i „ręczne” przemieszczanie punktów kontrolnych. Można także – pod warunkiem, że system CAD oferuje takie możliwości – zdefiniować wymagane rodzaje ciągłości pomiędzy kolejnymi płatami powierzchni, a system automatycznie dostosuje położenie kolejnych punktów, a dokładniej rzędów punktów kontrolnych. Co więcej, jeśli dla tych powierzchni została wcześniej zdefiniowana analiza rozkładu krzywizny Gaussa (lub jakakolwiek inna!), to wpływ każdej modyfikacji jest widoczny natychmiast w stosownych zmianach wyników tej analizy (Rys. 10). W rozważanym przykładzie, jeśli zdefiniowane są trzy powierzchnie (każda o innym stopniu swobody), to może się okazać, że liczba punktów kontrolnych powierzchni C w kierunku v (Nv=4) jest zbyt mała, aby zapewnić spełnienie warunków ciągłości z powierzchniami A i B. Dlaczego? – Odsyłam do opisu konstrukcji krzywej typu B-Spline („Elementarz cz. IV”). Jeśli ustalony jest warunek ciągłości G2 z powierzchnią B, to dla krawędzi wspólnej z powierzchnią A możliwy jest jedynie wybór pomiędzy G0 i G1 – trzeba zwiększyć stopień powierzchni C w kierunku v do d°=5 (6 punktów kontrolnych).

RYS. 10.

Możliwe jest także zastosowanie bardziej zaawansowanych funkcji, takich jak Match Surface (Rys. 11), która dostosowuje kształt powierzchni i sieć jej punktów kontrolnych do wskazanej krawędzi innej powierzchni z zachowaniem rodzaju ciągłości zdefiniowanej przez konstruktora, a w sytuacji zbyt dużych wymagań „podpowiada”: Your surface is over-constrained. Także i tu zmiana liczby punktów kontrolnych powierzchni C z N=4 na N=6 rozwiązuje problem – powierzchnia C może mieć ciągłość krzywizny z powierzchniami A i B.

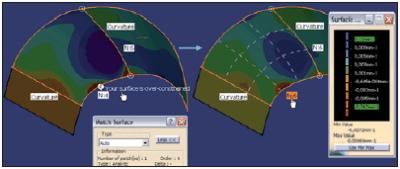
RYS. 11.

Jeśli, pomimo tych wszystkich zabiegów, jakość modelu powierzchniowego nie jest zadawalająca, to odsyłam na początek – powierzchnia jest tak dobra, jak dobre są krzywe! Bo tylko gładkie krzywe z równomiernymi zmianami krzywizny (Rys. 12) zapewnią dobrej jakości modele powierzchniowe projektowanych wyrobów.

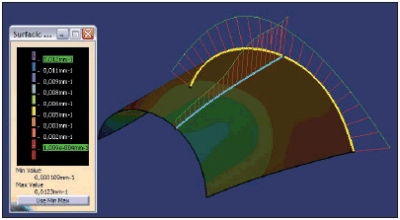
RYS. 12.

Podsumowanie

Mam nadzieję, że przekonałem sceptyków do tego, że model matematyczny krzywej lub powierzchni nie jest tylko przedmiotem badań teoretycznych. Czy można mówić o zaawansowanym modelowaniu powierzchniowym bez analizy jakości krzywych i powierzchni? Chyba nie, bo dopiero wnioski z takiej analizy prowadzą do wyboru innej metody, funkcji (innego modelu matematycznego) albo modyfikacji stopnia swobody krzywej (powierzchni), a świadomy wybór modelu lub stopnia swobody bez żadnych podstaw teoretycznych brzmi jakoś nielogicznie. Jednak, aby nie być posądzonym o przesadne teoretyzowanie muszę przyznać, że dzisiejsze systemy CAD coraz bardziej „zwalniają” konstruktora z patrzenia na model powierzchniowy kategoriami teoretycznych modeli matematycznych. Czy kiedykolwiek będzie tak, że w środowisku CAD można będzie definiować zaawansowane modele powierzchniowe bez znajomości teorii? Tego nie jestem pewien, ale z pewnością wiedza z zakresu teorii połączona z praktyką konstrukcyjną zawsze będzie wartościowa.

Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO