Jeszcze przed kilkoma laty konstruktor zajmujący się definiowaniem modeli powierzchniowych, szczególnie w zakresie zewnętrznych powierzchni estetycznych (karoseria samochodu, obudowa odkurzacza, itp.) musiał posiadać ogromną wiedzę z zakresu matematycznego opisu krzywych i powierzchni stosowanych w systemach CAD. Znajomość matematycznych mechanizmów zastosowanych w algorytmach obliczeniowych i powiązanych wprost z funkcjami, jakie ma do dyspozycji konstruktor, nie jest moim zdaniem głównym zadaniem konstruktora, bo powinien się on skupić na zdefiniowaniu takiego modelu geometrycznego, który spełnia wszystkie wymagania techniczne, technologiczne, estetyczne czy funkcjonalne
Rozwój aplikacji wspomagających modelowanie powierzchniowe prowadzi do zdefiniowania takiego interfejsu użytkownika, w którym konstruktor jest w coraz większym zakresie „zwolniony” z obowiązku wyboru typu krzywej lub powierzchni, czyli funkcji, jaką powinien zastosować. Wybór algorytmu jest coraz częściej dokonywany przez system CAD, w oparciu o wymagania zdefiniowane przez konstruktora. Przykłady takich wymagań można mnożyć:
-
Potrzebuję taką krzywą płaską, która połączy dwie inne krzywe. Krzywa łącząca musi mieć ciągły i jednorodny przebieg zmian krzywizny, a w punktach skrajnych musi zachować ciągłość typu G2 ze wskazanymi krzywymi. Co jest ważniejsze dla konstruktora: spełnienie powyższych wymagań czy zastosowanie wybranego typu krzywej, na przykład krzywej Béziera lub B-Spline? Która z tych krzywych najlepiej spełnia wymagania konstrukcyjne? Czy lepiej, aby konstruktor dokonywał takiego wyboru czy może system CAD?
-
Potrzebuję powierzchnię, która wypełni przestrzeń pomiędzy wskazanymi krzywymi granicznymi z zachowaniem ciągłości typu G0 wzdłuż jednej krzywej i ciągłości typu G2 wzdłuż innej. Powierzchnia typu UPBS czy NURBS? Czy stopień powierzchni w obu kierunkach głównych powinien być równy? Na te i podobne pytania „guru” modelowania powierzchniowego odpowie bez zastanowienia, bo przez lata dokonywał takiego wyboru. Ale jaka będzie odpowiedź… początkującego konstruktora?
RYS. 1
Czy w związku z tym można całkowicie zapomnieć o MATEMATYCE, która przecież gdzieś „w tle” bez udziału konstruktora decyduje o rezultacie zastosowania konkretnej funkcji? Czy dzisiejsze systemy CAD faktycznie „zwalniają” konstruktora ze znajomości teorii modelowania powierzchniowego? Moim zdaniem: i tak, i nie. Tak, bo – jak już napisałem wcześniej – wiele funkcji dzisiejszych systemów CAD dokonuje wyboru rodzaju krzywej lub powierzchni oraz ich parametrów w sposób automatyczny, a kryterium tego wyboru jest spełnienie wymagań zdefiniowanych przez konstruktora. Nie – bo taki automatyczny wybór nie zawsze jest najlepszy i konstruktor musi „ręcznie” zmodyfikować rozwiązanie proponowane przez system CAD. Na przykład zmienić stopień krzywej lub lokalnie zmodyfikować sieć punktów kontrolnych powierzchni, aby zapewnić lepszy rozkład zmian krzywizny.
No tak, ale co to jest stopień krzywej lub sieć punktów kontrolnych powierzchni? I tu powracamy do tytułowego „elementarza”, który powinien wyjaśnić przynajmniej podstawowe pojęcia modelowania powierzchniowego.
RYS. 2
W każdym systemie CAD możemy bez problemu narysować linię (płaską lub przestrzenną). Sytuacja się nieco komplikuje, kiedy trzeba zdefiniować krzywą. I nie mam tu na myśli typowych krzywych (okrąg, elipsa, parabola, itp.), których równania kanoniczne [F(x,y)=0 lub F(x,y,z)=0] są od wieków znane, a każda z nich może być precyzyjnie wykreślona. Możemy też wskazać kilka punktów krzywej, na przykład 3 punkty okręgu i bez znajomości jego równania jednoznacznie zdefiniować okrąg. Ale jak zdefiniować takie równanie dla dowolnej krzywej? Czy po wskazaniu kilku lub kilkunastu punktów można wygenerować równanie jednej krzywej? W tym miejscu chciałbym zwrócić uwagę, że w definicji krzywych dowolnych (swobodnych) istotne jest to, żeby przechodziła ona przez ograniczoną liczbę punktów (na przykład tylko punkt początkowy i końcowy) oraz aby była „gładka”. Trzeba też zauważyć, że wraz ze wzrostem liczby zadanych punktów krzywej jej równanie(a) staje się coraz bardziej złożone. A to w kontekście algorytmów oznacza więcej czasu na obliczenia. Ale problemem jest nie tylko równanie, bo krzywa musi być nie tylko precyzyjnie zdefiniowana, ale jej model matematyczny musi także umożliwiać w miarę lokalne modyfikacje (na przykład w celu uzyskania lepszego rozkładu zmian krzywizny), zapewnić „gładkość”, możliwość obliczenia pochodnych w dowolnym punkcie (ciągłość typu G1, G2, G3), stabilność po zmianie kryteriów konstrukcyjnych oraz łatwość wizualizacji. Dlatego w systemach CAD zastosowano parametryczną definicję krzywej:
-
F: [0,1] → (f(u), g(u)) – dla krzywej płaskiej,
-
F: [0,1] → (f(u), g(u), h(u)) – dla krzywej przestrzennej,
gdzie:
f, g i h są wielomianami,
a u jest parametrem z zakresu [0,1].
RYS. 3
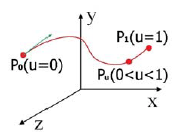
Kształt takiej krzywej jest określony przez jej punkty skrajne (początek i koniec) oraz funkcje f, g, h, które opisują charakter zmian współrzędnych x, y i z dowolnego punku krzywej – gdzieś pomiędzy jej początkiem i końcem. Napisałem „gdzieś”, bo istnieje nieskończenie wiele krzywych swobodnych „rozpiętych” na dwóch lub więcej punktach. Czy wobec tego, wracając do świata CAD, należałoby powiedzieć, że system arbitralnie wybiera jedną spośród wielu teoretycznie możliwych krzywych? W pewnym uproszczeniu można odpowiedzieć twierdząco, choć oczywiście zależy to od systemu i algorytmu realizowanego przez wybrane polecenie. W systemach CAD powszechnie zastosowanie znalazły krzywe Béziera. Użytkownik systemu CAD nie widzi równań takiej krzywej, bo dla niego nie są one istotne. Zamiast równań widzi (i ma możliwość ich modyfikacji) punkty kontrolne krzywej lub inaczej wielobok kontrolny.
RYS. 4
Rozważmy przykład takiej krzywej z 4 punktami kontrolnymi (P0, P1, P2 i P3):
-
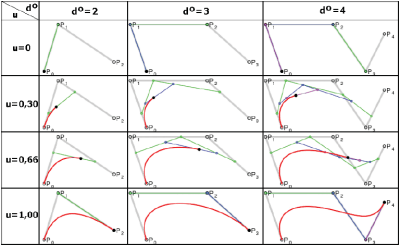
Liczba punktów wieloboku kontrolnego decyduje o tak zwanym stopniu swobody krzywej (d°). Mówimy, że krzywa jest stopnia N, jeśli jest opisana przez N+1 punktów kontrolnych.
-
Punkty P0 i P3 definiują początek i koniec krzywej, czyli krzywa ma zwrot od P0 do P1 (u = 0 dla P0 i u = 1 dla P1).
-
Punkt P1 określa wektor styczności tej krzywej w jej punkcie początkowym, a punkt P3 w punkcie końcowym.
-
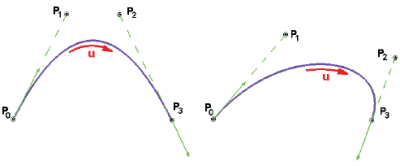
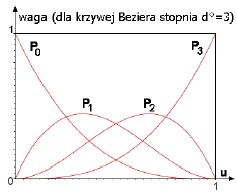
Krzywa Béziera nie przechodzi przez punkty P1 i P2, ale każdy z tych punktów wpływa na kształt krzywej, bo dla dowolnego u jest określona siła „przyciągania” krzywej przez każdy punkt kontrolny (inaczej: waga punktu – przyp. autora).
-
Przesunięcie jednego z punktów kontrolnych wpływa na kształt całej krzywej, choć najbardziej w tej części krzywej, która jest najbliżej modyfikowanego punktu kontrolnego, bo jego waga w tym punkcie krzywej jest największa. Funkcje definiujące wagi są obliczane automatycznie przez algorytm definiujący krzywą Béziera i nie mogą być modyfikowane.
-
Możliwa jest modyfikacja położenia punktów P0 i P3, ale zazwyczaj nie ma takiej potrzeby, bo początek i koniec krzywej wynika z wymagań konstrukcyjnych.
Choć maksymalna liczba punktów kontrolnych teoretycznej krzywej Béziera nie jest ograniczona, to praktyczne zastosowanie znajdują krzywe, które są opisane przez 2 do 6 punktów kontrolnych – zazwyczaj nie więcej niż 16. Do wieloboku kontrolnego krzywej Béziera zawsze można dodać nowy punkt, czyli każdą krzywą stopnia N można zamienić na krzywą stopnia N+1 bez zmiany kształtu krzywej. Oczywiście, wraz ze wzrostem liczby punktów kontrolnych, czyli stopnia krzywej rośnie możliwość zdefiniowania bardziej skomplikowanej krzywej oraz możliwości modyfikacji jej kształtu. Ale nie zawsze jest możliwe działanie odwrotne, bo zmniejszenie stopnia krzywej skutkuje zazwyczaj wygenerowaniem krzywej, która różni się od krzywej pierwotnej. I nie ma w tym nic złego, pod warunkiem, że różnice… mieszczą się w zakresie akceptowalnym przez konstruktora.
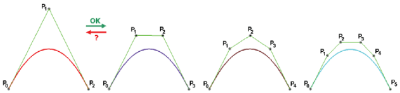
RYS. 5
Czy krzywa Béziera może być zastosowana w definiowaniu skomplikowanych krzywych? Czy 16 punktów kontrolnych zawsze wystarczy do spełnienia wszystkich wymagań konstrukcyjnych? Z pewnością nie. Dlatego w systemach wspomagających modelowanie powierzchniowe, aby uniknąć bardzo skomplikowanych równań opisujących kształt krzywych złożonych stosuje się pewien wybieg. Jedną skomplikowaną krzywą można przecież…
Kontynuacja tematu w następnym odcinku cyklu „Elementarz”.
Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO





