Kontynuując temat rozpoczęty w poprzednim numerze Design News, proponuję kilka uwag na temat analizy jakości modelu powierzchniowego
Podobnie jak w przypadku krzywych model powierzchniowy części można analizować pod kątem różnych rodzajów ciągłości:
-
ciągłość geometryczna (G0): dwie powierzchnie mają wspólną krawędź i ponadto w obszarze ?wspólnym? nie ma żadnych szczelin;
-
ciągłoś ć styczności (G1): dwie powierzchnie ciągłe według kryterium G0 są wzajemnie styczne w każdym punkcie krawędzi wspólnej;
-
ciągłoś ć krzywizny (G2): dwie powierzchnie ciągłe według kryterium G1 mają taki sam promień krzywizny w każdym punkcie krawędzi wspólnej;
-
ciągłość gradientu zmian krzywizny (G3): dwie powierzchnie ciągłe według kryterium G2 mają w obszarach przyległych do krawędzi wspólnej podobny charakter (gradient) zmian krzywizny.
Zanim jednak rozważymy metody analizy jakości powierzchni warto zastanowić się chwilę nad metodami definiowania modelu powierzchniowego, bo jakość powierzchni, a także możliwości analizy jej jakości są wprost powiązane z jej przeznaczeniem. Nie ma przecież uzasadnienia, aby klasyczne powierzchnie mechaniczne, na przykład takie, które definiują kształt odkuwki, miały ciągłość typu G2. Z drugiej strony trudno zaakceptować powierzchnię, która określa kształt obudowy zewnętrznej odkurzacza bez ciągłości typu G2, bo jeśli będzie ona ciągła tylko w zakresie G1, to estetyczne walory obudowy wykonanej w oparciu o taką powierzchnię będą ? co najmniej ? wątpliwe. W tym kontekście możemy więc mówić o przynajmniej dwóch rodzajach projektowanych powierzchni: powierzchniach mechanicznych i powierzchniach stylistycznych. W projektowaniu powierzchni mechanicznych ? czyli wtedy, gdy istotna jest jedynie ciągłość typu G0 i G1 ? walory estetyczne takie jak na przykład rozkład krzywizny, nie mają praktycznego uzasadnienia. W przypadku powierzchni stylistycznych, dla których estetyka jest kryterium najważniejszym, ciągłość typu G1 to za mało i dlatego zazwyczaj ciągłość typu G2 (tylko czasami G3) musi być zapewniona. Z powodów wymienionych powyżej różne rodzaje analizy jakości powierzchni są dostępne w różnych środowiskach projektowania powierzchniowego
Procedura analizy jakości powierzchni jest taka sama jak w przypadku analizy jakości krzywych (patrz ?Elementarz modelowania powierzchniowego cz. I?). W pierwszym kroku trzeba sprawdzić ciągłość modelu powierzchniowego, a potem rozkład krzywizny analizowanej powierzchni. Ciągłość geometryczna (G0) może być oceniona wzrokowo, ale zazwyczaj obszary nieciągłości są tak małe, że trudno jest je zauważyć gołym okiem. Zakładam oczywiście, że konstruktor przykłada się do swojej pracy i nie tworzy modelu powierzchniowego ?na oko?.
Weźmy na przykład dwie powierzchnie, które ?na oko? mają wspólną krawędź, czyli ?na oko? są ciągłe według kryterium G0. Dlaczego ciągłość geometryczna modelu powierzchniowego jest tak ważna? Otóż dlatego, że model powierzchniowy części jest zazwyczaj wykorzystany na kolejnych etapach procesu projektowego, na przykład w modelowaniu bryłowym lub definiowaniu technologii obróbki na obrabiarce CNC. Jeśli powierzchnia nie jest ciągła, to bryła zbudowana na takiej powierzchni może być również nieciągła lub w najgorszym przypadku definicja takiej bryły może okazać się niemożliwa (Rys. 1). Podobnie tor ruchu freza jest wprost związany z jakością definicji powierzchni obrabianej.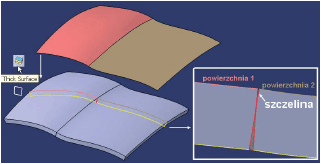
Rys. 1.
Czy zawsze trzeba dążyć do perfekcyjnej definicji krzywych i powierzchni?
Niektóre systemy CAD oferują możliwość korygowania niewielkich defektów geometrycznych w zakresie tolerancji zdefiniowanej przez użytkownika (Tolerant Modeling), a rezultat operacji połączenia dwóch płatów powierzchni w jeden obiekt może być różny, w zależności od ustawień. Załóżmy, że te dwie powierzchnie nie mają wspólnej krawędzi, a maksymalna odległość sąsiadujących krawędzi (szerokość szczeliny) to 0,096 mm (Rys. 2).
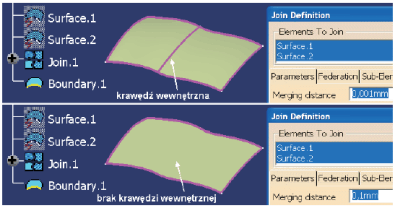
Rys. 2
Jeśli tolerancja połączenia tych dwóch powierzchni (Merging distance) jest równa 0,001mm, to rezultat połączenia (Join) ma krawędź wewnętrzną, czyli szczelinę. Jeśli ta tolerancja jest większa od 0,096mm (na przykład 0,1mm), to rezultat połączenia dwóch powierzchni nie ma krawędzi wewnętrznej, bo wszystkie szczeliny, których szerokość jest mniejsza od wartości parametru Merging distance są automatycznie korygowane. Trzeba jednak zaznaczyć, że jest to jedynie operacja topologiczna, a definicja powierzchni składowych pozostaje niezmieniona. Lepiej więc zmodyfikować geometrię jednej lub obu powierzchni tak, aby uzyskać żądaną ciągłość.
Jak poprawić niedoskonałości modelu powierzchniowego? Odpowiedź zależy od tego, jak powierzchnie zostały zdefiniowane. Jeśli są to powierzchnie mechaniczne, które zazwyczaj są zbudowane na krzywych parametrycznych, to można odpowiednio zmienić wartości parametrów krzywych i powierzchni. Jeśli powierzchnie zdefiniowano w środowisku modelowania swobodnego (FreeStyle), to stosowne modyfikacje mogą być uzyskane na przykład przez modyfikację punktów kontrolnych krzywych/powierzchni lub wprost przez zadanie rodzaju wymaganej ciągłości i ustalenie wszystkich dodatkowych ograniczeń (polecenia typu Match Surface ? Rys. 3).
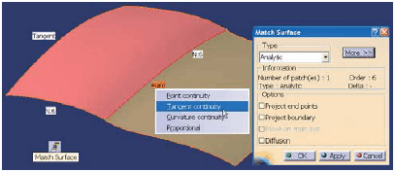
Rys. 3
W niektórych systemach możliwe jest też zdefiniowanie rodzaju wymaganej ciągłości, maksymalnej dopuszczalnej deformacji powierzchni i jej globalna lub lokalna naprawa (Healing), a nie modyfikacja parametrów powierzchni zastosowanych w jej definicji.
Analizę ciągłości modelu powierzchniowego wspomagają narzędzia typu Connect Checker (Rys. 4). Tu jeszcze raz podkreślam, że jest to tylko analiza, czyli wskazanie niezgodności z wybranym (Distance=G0, Tangency=G1, Curvature=G2) kryterium ciągłości. Rolą konstruktora jest ustalić czy, w jakim zakresie i jak należy zmodyfikować model powierzchniowy.
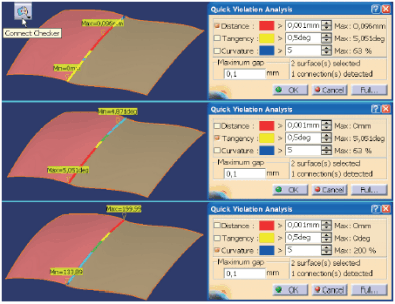
Rys. 4
Jeśli model powierzchniowy jest ciągły, to można przystąpić do analizy jakości rozkładu krzywizny. Także i tu można wizualnie ocenić jakość powierzchni (Rys. 5), na przykład ostre krawędzie (brak ciągłości typu G1) lub niepożądane wgniecenia (lokalne zmiany znaku krzywizny).
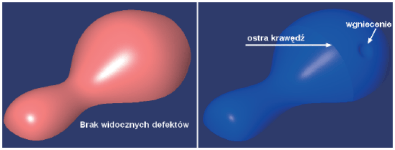
Rys. 5
Analiza wizualna to oczywiście za mało do oceny rozkładu krzywizny modelu powierzchniowego. Zanim jednak przejdę do omówienia niektórych metod oceny rozkładu krzywizny, należy zdefiniować, czym jest krzywizna powierzchni. W teorii modelowania powierzchniowego stosujemy najczęściej wartość średnią nazywaną krzywizną Gaussa, którą znajdujemy stosując następującą procedurę:
-
W każdym punkcie powierzchni można zdefiniować prostą do niej prostopadłą.
-
Przez tak wyznaczoną linię można poprowadzić nieskończenie wiele płaszczyzn.
-
Płaszczyzny te mogą posłużyć do wyznaczenia nieskończenie wielu krzywych = przekrojów powierzchni, a każda z tych krzywych ma określony rozkład krzywizny.
-
Dla każdego punktu powierzchni (dla różnych przekrojów) można znaleźć największy promień krzywizny (R1) i najmniejszy promień krzywizny (R2).
-
Krzywizna Gaussa (KG) może być obliczona zgodnie z równaniem:
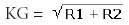
Ponadto, jeśli promienie R1 i R2 mają środki po tej samej stronie analizowanej powierzchni, to krzywizna jest dodatnia, a w przeciwnym przypadku ujemna (Rys. 6).
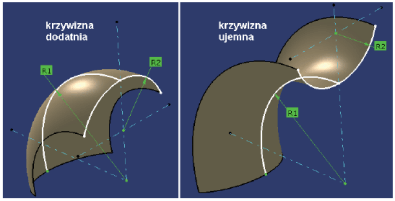
Rys. 6
Narzędzia, które w systemach CAD wspomagają analizy rozkładu krzywizny powierzchni (na przykład Surfacic Curvature Analysis) umożliwiają zazwyczaj badanie rozkładu krzywizny Gaussa. W tym przypadku nie jest istotna wartość krzywizny jako takiej, ale charakter zmian krzywizny na całej powierzchni. Dobra powierzchnia to taka, na której nie występują nagłe zmiany, czyli małe (wąskie) obszary przejścia z małej krzywizny do dużej krzywizny.
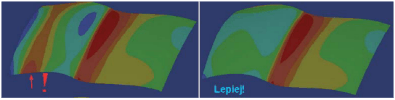
Rys. 7
Trzeba też zauważyć, że nagła zmiana znaku krzywizny w pewnym obszarze powierzchni oznacza, że powierzchnia ma wgłębienie lub wybrzuszenie, co z reguły oznacza defekt, który powinien zostać naprawiony (Rys. 7). W tym zakresie możliwa jest uproszczona analiza krzywizny (Inflection Area), której rezultatem jest identyfikacja obszarów z krzywizną dodatnią (kolor niebieski) i ujemną (kolor zielony) – patrz Rys. 8.
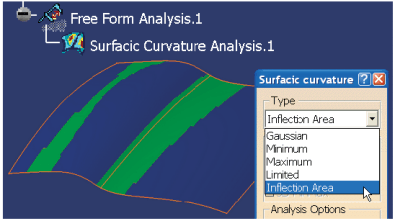
Rys. 8
Czasami zachodzi potrzeba szczegółowej analizy nie tylko przebiegu zmian krzywizny, ale także wartości krzywizny lub promienia krzywizny. Można to zrobić w dowolnie wskazanym punkcie lub wykonać taką analizę dla krzywej = przekroju powierzchni. Parametryzacja położenia płaszczyzny przekroju umożliwia analizę krzywizny powierzchni w każdym z możliwych przekrojów. Funkcja Porcupine Analysis (Rys. 9) zastosowana do takiej analizy została omówiona w poprzednim odcinku.
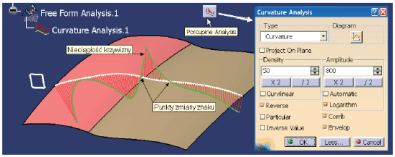
Rys. 9
Jeśli konieczna jest analiza zmian krzywizny wzdłuż kilku krzywych (przekrojów powierzchni), to można zastosować funkcję Cutting Planes. Rezultat jest podobny do tego, jaki można uzyskać wykonując polecenie Porcupine Analysis, tyle że możliwe jest łatwe (bo kontrolowane położeniem kompasu) ustalenie położenia płaszczyzn tnących, ich liczby oraz odległości między nimi (Rys. 10).
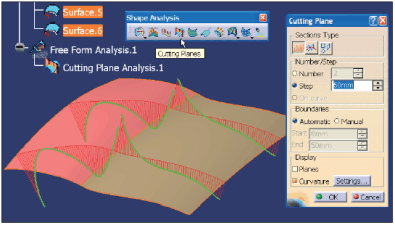
Rys. 10
I wreszcie dla tych, którzy tworzą powierzchnie stylistyczne, dostępnych jest kilka bardziej zaawansowanych możliwości analizy ciągłości typu G2. Najbardziej typowa z nich to analiza refleksów świetlnych na powierzchni. Liniowe źródła światła, których liczbę i odległość, a także położenie w przestrzeni 3D można swobodnie zmieniać znajdują swoje odbicie na analizowanej powierzchni. Jeśli dwie powierzchnie są ciągłe według kryterium G2, to także krzywe refleksów świetlnych (odbicia liniowych ?świetlówek?) są na tej powierzchni ciągłe (Rys. 11)

Rys. 11
Ostatnią z analiz jakości powierzchni, potwierdzającą jej walory estetyczne może być analiza typu Environment Mapping, w której model powierzchniowy jest umieszczony w wirtualnym środowisku. To środowisko jest zdefiniowane jako dowolny obraz płaski, a analizowana powierzchnia jak lustro odbija obraz tego środowiska. Rezultat takiej analizy pozwala bardzo intuicyjnie ocenić estetyczną jakość powierzchni i jednocześnie wskazać potencjalne obszary wymagające korekty (Rys. 12).

Rys. 12
Podsumowanie
1. Perfekcyjny ?na oko? model powierzchniowy może być zupełnie nieprzydatny.
2. Wybór funkcji, ustalenie wartości parametrów i zdefiniowanie ograniczeń wpływa nie tylko na jakość modelu powierzchniowego, ale także na możliwości jego modyfikacji.
3. W procesie tworzenia modelu powierzchniowego nie można zapomnieć o analizie jego jakości.
4. Wymagana jakość modelu powierzchniowego (rodzaj ciągłości oraz rozkład krzywizny) wynika wprost z rodzaju projektowanej części.
Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO





