Jak rozwiązać trudny problem nieliniowy

Kierowany przeze mnie zespół inżynierów zmierzył się ostatnio z jednym z naprawdę trudnych problemów analitycznych, w przypadku którego można byto zastosować jedynie kilka upraszczających przypuszczeń, lecz żadnego klasycznego podejścia. Byt to jeden z problemów, które stają się coraz bardziej typowe, co odzwierciedla skomplikowaną naturę wielu wyzwań analitycznych spotykanych w świecie rzeczywistym.

Powierzono nam zadanie udoskonalenia projektu nadmuchiwanego systemu zabezpieczającego, opartego na polimerowej powłoce z jednorodnego (nietkanego) materiału. Materiał, z którego wykonano powłokę, był bardzo elastyczny – jak papier, w tej aplikacji jednak zdecydowanie bardziej wszechstronny i wytrzymały. Nasze zadanie: dla danej wielkości powłoki wybrać optymalny gatunek materiału nietkanego – tak, aby system bezpieczeństwa mógł wytrzymać wewnętrzne wyrównane ciśnienie do 0,9 bara bez rozerwania.

Krok 1. Co wiemy

Zaczęliśmy od zastanowienia się, co wiemy. Faktów było mało. Znaliśmy płaskie wymiary kilku wielkości nienadmuchanych powłok. Mieliśmy trochę danych o specyfikacjach kilku gatunków materiałów, jakie można by zastosować. Dane te obejmowały: grubość oraz krzywe rozciągania jednoosiowego do rozerwania próbki. W wyniku przeprowadzonych testów badawczych udało nam się ustalić, że powłoki można rozciągnąć do około 20% (ciśnienie zbliża się wtedy do wartości, przy której powłoka pęka). Wynik ten nas zaskoczył, ponieważ z testów na rozciąganie jednoosiowe wynikało, że materiał rozrywał się przy znacznie niższych wartościach. Ponadto odkryliśmy, że podawane ciśnienie rozrywania wg skali Mullena (standard przemysłowy TAPPI służący do mierzenia punktu rozrywania płaskich struktur) dla materiału wykazywało ok. 100% zmienności, podczas gdy zmienność, którą nam się udało zaobserwować podczas nadmuchiwania powłok aż do ich rozerwania, była znacznie niższa. W końcu wiedzieliśmy, że klasyczne równania do projektowania zbiorników ciśnieniowych są zbyt uproszczone, żeby dało się przeprowadzić właściwe analizy, ponieważ dają zbyt niskie oszacowania naprężenia i odkształcenia – aż o ok. 300%!

Krok 2. Decyzja, czy modelowanie może pomóc

Ręczne nadmuchiwanie powłoki – próbki za pomocą słomki do napojów dało nam wgląd w czekające nas wyzwania. Skomplikowany, nadmuchany kształt, na którym było dużo wybrzuszeń (zmarszczek) sugerował, że największe szansę na powodzenie analizy mamy przy zastosowaniu Dynamicznej Funkcji Jawnej (Explicit Dynamics), która jest szczególnym przypadkiem nieliniowej analizy FEA (Analiza Metodą Elementów Skończonych – Finite Element Analysis), popularnej wśród inżynierów pracujących w motoryzacji, a stosowanej do przeprowadzania symulacji wypadków samochodowych i załączania się poduszek powietrznych.

^{CZY TO MOŻNA MODELOWAĆ?}

Model FEA nadmuchiwał się bardzo podobnie jak prawdziwa powłoka, łącznie ze wszystkimi skomplikowanymi fałdami i wybrzuszeniami. Początkowe prace poszukiwawcze trwały kilka dni, aż w końcu doszliśmy do wniosku: „Tak, to może być modelowane”

Po pierwsze należało ustalić, czy można sporządzić model FEA powłoki napełnionej powietrzem jak w naszym doświadczeniu ze słomką. Posługując się danymi materiałowymi jednoosiowych testów, zbudowaliśmy model ABAQUS/ Explicit FEA płaskiej powłoki, po czym przeanalizowaliśmy go przy zwiększaniu wewnętrznego ciśnienia do 0,06 bara (szacunkowa wartość ciśnienia, jakim wypełniliśmy testową powłokę za pomocą naszych płuc). Model FEA nadmuchiwał się bardzo podobnie jak prawdziwa powłoka, łącznie ze wszystkimi skomplikowanymi fałdami i wybrzuszeniami. Początkowe prace poszukiwawcze trwały kilka dni, aż w końcu doszliśmy do wniosku: „Tak, to może być modelowane”.

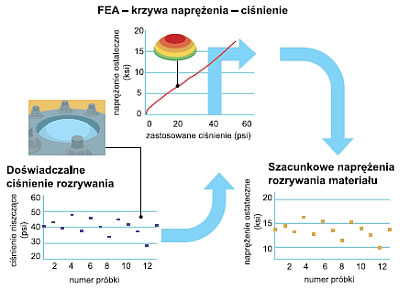
^{Poprawianie charakterystyki wytrzymałości materiału}

Dane z próby pęcherzykowej zostały połączone z nieliniowym modelem FEA w celu poprawy ostatecznej granicy wytrzymałości materiału, łącznie ze zmiennoscią statystyczną. W próbie pęcherzykowej przetestowano wiele próbek materiałów, dla każdej odnotowywano wartość ciśnienia niszczącego. Nieliniowy model FEA testu pęcherzykowego został obliczony w celu otrzymania ogólnej zależności pomiędzy ciśnieniem próby a naprężeniem materiału. Dyskretne dane FEA zostały wprowadzone do programu obliczeniowego Mathcad, który stosuje krzywe składane oraz dopasowywanie krzywej do obliczania nieliniowej funkcji przenoszenia zależności pomiędzy ciśnieniem nadmuchiwania a naprężeniem materiału. Na koniec wszystkie wartości ciśnienia rozrywania pochodzące z fizycznej próby pęcherzykowej zostały przekonwertowane na estymacje naprężeń materiału (jedna wartość dla każdej testowanej próbki) przy zastosowaniu nieliniowej funkcji przenoszenia. W opisywanym przykładzie przetestowano 12 próbek i ustalono 12 wartości ostatecznych naprężeń materiału, które następnie zostały zastosowane do statystycznych estymacji zmienności ostatecznych naprężeń.

Krok 3. Określenie charakterystyki materiału

Musieliśmy uwzględnić dwie kłopotliwe sprzeczności związane z zachowaniem się materiału:

1. Naprężenia niszczące prób na rozrywanie jednoosiowe były znacznie niższe od wartości wytrzymałości na rozrywanie, mierzonych podczas testów rozsadzania powłok.

2. Testy Mullena sugerowały, że materiały powinny wykazywać znacznie większą zmienność wyników testów rozrywania pod ciśnieniem, niż zostało to zaobserwowane podczas rzeczywistych testów.

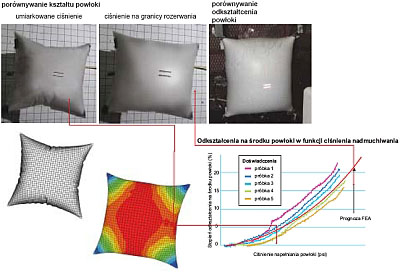
^{Nadmuchać, aż pękną!}

Nadmuchiwaliśmy powłoki aż do ich pęknięcia, po czym porównywaliśmy zarówno kształty powłok, jak i zachodzące w nich odkształcenia z modelem FEA. Przy niskim i umiarkowanym ciśnieniu nadmuchiwania widoczne były pomarszczenia na zewnętrznych brzegach. Przy wyższych ciśnieniach pomarszczenia znikały. Bezkontaktowy laserowy tensometr pomaga w oszacowaniu modelu ilościowego poprzez odnotowywanie odkształceń podczas wykonywania testów na wielu próbkach. Przewidywania modelu FEA dla tej ilości były doskonałe. Należy zauważyć, że były to przewidywania z modelu FEA, a nie dopasowywanie krzywej do zmierzonych parametrów odkształcenia powłoki.

Podczas kontroli wizualnej jednorodnego materiału okazało się, że jego powierzchniowa jednorodność była nieregularna, co powodowało, że materiał miał mocne i słabe punkty. Podczas prób rozrywania jednoosiowego długi, cienki pasek testowy zawsze przerywał się w słabym miejscu (jak przysłowiowe słabe ogniwo łańcucha). Jednakże w przypadku dwuwymiarowego obciążenia powłoki podczas nadmuchiwania tworzyły się różne obciążenia na powierzchni powłoki, co sprawiało, że struktura była mniej podatna na syndrom „najsłabszego ogniwa”. W powłoce o kształcie koperty słabe obszary w materiale były wzmacniane sąsiadującymi z nimi obszarami mocniejszymi. To wyjaśnia, dlaczego na podstawie naprężeń niszczących w teście na rozrywanie jednoosiowe zbyt niska była ocena rzeczywistych naprężeń niszczących podczas nadmuchiwania powłoki. Udało nam się ustalić, że problem z danymi pochodzącymi z testu Mullena polegał na protokole testowym, zgodnie z którym próbki musiały mieć średnicę 2,54 cm. Dla naszego materiału taka wielkość była reprezentatywna (słabe i mocne miejsca). Dlatego podczas testu Mullena łatwo było otrzymać próbkę zawierającą tylko słabe lub tylko mocne miejsca; co w rezultacie dawało duży zakres zmienności podczas wykonywania testów na rozrywanie. Jednakże przy testowaniu typowej powłoki, o wymiarach powiedzmy 25×25 cm (a więc w miarę dużej), mocniejsze miejsca przejmowały obciążenia przypadające na miejsca słabsze, w ten sposób znacznie redukując widoczną zmienność ciśnienia potrzebnego do rozerwania powłoki.

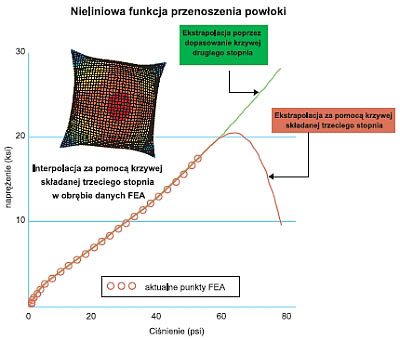
^{Udało się!}

Przy zastosowaniu krzywych składanych sześciennych oraz dopasowywaniu krzywych w celu utworzenia pseudoanalitycznych funkcji z danych dyskretnych należy zachować ostrożność. Powyższy obraz pokazuje, w jaki sposób ekstrapolacja danych może w połączeniu z krzywymi składanymi trzeciego stopnia przynieść fatalne wyniki. Ekstrapolacja za pomocą krzywej drugiego stopnia, w której jedynie kilka ostatnich punktów wykorzystano do obliczenia współczynników dopasowywania krzywej, dała słuszne odwzorowanie. Oba odwzorowania można było łatwo połączyć, stosując logikę „jeśli” Mathcada.

Obserwacje te doprowadziły nas do zastąpienia danych otrzymanych z testu na rozrywanie Mullena danymi otrzymanymi z naszych własnych „prób pęcherzykowych”, wielkowymiarowej wersji testera Mullena. Średnica naszego próbnika została ustawiona na 15 cm, co zapewniało wystarczające wzmocnienie „sąsiadujących” obszarów materiału w stopniu odpowiadającym wielkości badanych kopert. Niestety, ani za pomocą prób pęcherzykowych, ani testu Mullena nie dało się bezpośrednio określić ostatecznych naprężeń materiału. Można było tylko oszacować odkształcenia pęcherzyków oraz wartość podanego do pęcherzyków ciśnienia, łącznie z ciśnieniem pękania.

Zarówno w teście Mullena, jak i naszym teście pęcherzykowym płaska okrągła próbka materiału jest utwierdzona (dociśnięta) na obwodzie i nadmuchiwana, aż uzyska kształt pęcherzyka. Natura takiej deformacji: przy każdej wartości ciśnienia naprężenie i odkształcenie na powierzchni pęcherzyka będą różne (w przeciwieństwie do idealnego rozciągania jednoosiowego lub idealnego nadmuchiwania w teście sferycznym, w których dla danego obciążenia są jednolite naprężenia). W przypadku materiału o jednolitej strukturze maksymalne odkształcenie pęcherzyka wystąpi na środku górnej części pęcherzyka. W przypadku materiału niejednorodnego, w którym występują różnice struktury powierzchniowej, odkształcenie wystąpi w pobliżu środka wierzchołka pęcherzyka. Po przeanalizowaniu danych otrzymanych z testu rozciągania jednoosiowego oraz testu pęcherzykowego, w połączeniu z nieliniowymi modelami FEA testu pęcherzykowego, byliśmy w stanie określić praktyczne podejście do modelowania statystycznej zmienności zachowania się materiału. Wykorzystaliśmy dane jednoosiowe w celu określenia kształtu krzywej nieliniowego naprężenia/odkształcenia oraz parametry pękania materiału pochodzące z testu pęcherzykowego w celu określenia granicy naprężeń i odkształceń niszczących. Ponieważ dane dotyczące wytrzymałości na rozrywanie otrzymane z testu pęcherzykowego wychodziły poza dane z testu rozrywania jednoosiowego, po prostu wykonaliśmy ekstrapolację (za pomocą dobierania krzywej drugiego stopnia) danych pochodzących z prób rozrywania jednoosiowego. Następnie do weryfikacji tego podejścia zastosowaliśmy nieliniowe modele FEA rzeczywistych testów pęcherzykowych.

Określiliśmy charakterystykę poszczególnych materiałów w następujący sposób: pojedynczy, nieliniowy model FEA testu nadmuchiwania pęcherzyków został wykonany dla danych pochodzących z testu rozciągania jednoosiowego z ekstrapolacją, jednakże bez doprowadzenia do stanu zniszczenia. Uzyskaliśmy w ten sposób ogólną zależność pomiędzy ciśnieniem napełniania bąbelków a prognozowanym naprężeniem/odkształceniem pęcherzyka na środku.

Z modelu pary dyskretnych danych FEA wartości odkształcenia i naprężenia na środku pęcherzyka w zależności od zastosowanego ciśnienia zostały następnie zaimportowane do programu Mathcad służącego do obliczeń inżynieryjnych. W programie Mathcad łatwo było zdefiniować pseudoanalityczne przedstawienie tej nieliniowej funkcji przenoszenia, przy zastosowaniu interpolacji krzywej składanej trzeciego stopnia oraz dopasowywania krzywej. Na koniec wartości ciśnienia rozrywania materiału dla pewnej liczby próbek testowych zostały zmierzone za pomocą testu pęcherzykowego i wprowadzone do arkusza Mathcad, gdzie nieliniowa funkcja przenoszenia została zastosowana do określenia ciśnienia rozrywania, do oszacowania ostatecznych wartości naprężeń. Dzięki zastosowaniu tego podejścia rzeczywiste fizyczne wartości rozrywania materiału (oraz ich odchylenia) były konwertowane do wartości naprężenia powodującego rozerwanie poszczególnych próbek, pod wpływem obciążenia podobnego do rzeczywistych warunków materiału powłoki.

Podstawowa cecha tej metodologii: cała zmienność materiału została zgrupowana w zachowaniach niszczących, kształt podstawowej krzywej naprężenia/ odkształcenia stanowił średnie odwzorowanie. Doprowadziło to do znacznego uproszczenia oraz zwiększenia wydajności zarówno analizy charakterystyki materiału, jak i powłoki. W porównaniu z metodą sporządzania wielu modeli FEA z zastosowaniem przypadkowych słabych i mocnych części materiału i wykonania analizy Monte Carlo – nasza metoda z zastosowaniem nieliniowej funkcji przenoszenia, z wykorzystaniem jednego modelu FEA dla danej klasy materiału okazała się słusznym podejściem pragmatycznym.

Krok 4. Uzasadnienie modelu

Aby dokonać dalszego uwiarygodnienia naszego modelu nadmuchiwania powłoki, porównaliśmy wyniki nadmuchiwania powłoki z naszymi przewidywaniami z modelu FEA, w którym zastosowaliśmy udoskonalone odwzorowanie materiałowe. Rozpatrywaliśmy kształt powłoki podczas nadmuchiwania, obciążenia miejscowe mierzone na środku powłoki oraz ciśnienie rozrywania.

Otrzymaliśmy statystyczne dane szacunkowe ciśnienia rozrywania na bazie modelu FEA, poprzez zastosowanie techniki nieliniowej funkcji przenoszenia podobnej do tej, która była zastosowana do analizy pęcherzykowej. Jednak w tym przypadku sporządziliśmy nieliniowe funkcje przenoszenia przy zastosowaniu danych o naprężeniach i odkształceniach modeli powłoki (jeden model dla każdego materiału oraz rozmiaru powłoki) do określenia ostatecznych granic wytrzymałości (otrzymanych z testów pęcherzykowych) powłoki na nadmuchiwanie oraz ciśnienia w momencie rozrywania powłoki. Badania weryfikacyjne udowodniły, że podejście analityczne dobrze scharakteryzowało system oraz można je łatwo zastosować do oszacowania rodzajów materiałów oraz kształtów powłok.

Autor artykułu, dr Ted Diehl, jest autorytetem w dziedzinie strukturalnej mechaniki nieliniowej, uznanym przez międzynarodowe społeczności programów ABAQUS i Mathcad na całym świecie. Przez ostatnie trzy lata Diehl zajmuje się analizami nowoczesnych materiałów firmy DuPont oraz ich zastosowaniem w nowych, unikatowych aplikacjach użytkowych. Przed podjęciem pracy dla DuPont Diehl przez pięć lat pracował dla firmy Motorola oraz osiem lat w Eastman Kodak.