Parametryczna definicja krzywej (Polynomial curve), omówiona w poprzednim odcinku ?Elementarza? na przykładzie krzywej Béziera, jest najlepszym z możliwych modeli matematycznych stosowanych w systemach CAD. Najlepsza nie tylko dlatego, że funkcje wielomianowe zastosowane w tym modelu dają się łatwo zastosować w algorytmach komputerowych, ale także dlatego, że krzywe parametryczne można łatwo modyfikować, bo położenie każdego punktu krzywej jest opisane współrzędną liczoną po łuku tej krzywej od innego punktu tej krzywej, na przykład punktu początkowego. Ta cecha nabiera szczególnego znaczenia wtedy, gdy trzeba znaleźć punkt przecięcia krzywych lub gdy krzywa teoretyczna musi być przycięta do/od jakiegoś punktu na krzywej
Model matematyczny krzywej Béziera, jakkolwiek łatwy do zastosowania w systemach CAD, jednak ma swoje wady. W przypadku skomplikowanych krzywych konstrukcyjnych zwiększanie liczby punktów kontrolnych krzywej ? czyli także stopnia wielomianu, który jest modelem matematycznym krzywej ? implikuje dłuższy czas obliczeń oraz, co wydaje się być ważniejsze, utrudnia kontrolę kształtu krzywej ? nawet niewielkie zmiany współczynników mogą wpływać na jej globalny kształt. Wraz ze wzrostem stopnia wielomianu rośnie liczba jego lokalnych minimów i maksimów ? także tych ?niechcianych?. Na przykład parabola (krzywa 2-stopnia) ma tylko jedno minimum, a krzywa 3-stopnia może ich mieć aż dwa. Reasumując można powiedzieć, że praktyczne zastosowanie krzywych Béziera jest ograniczone, bo:
-
jeśli zadaniem konstruktora jest zdefiniowanie krzywej gładkiej z gwałtownymi i lokalnymi zmianami krzywizny (RYS. 1), to aby spełnić wymagania konstrukcyjne konieczne jest zastosowanie równań wysokiego stopnia ? jednorodny rozkład punktów kontrolnych krzywej zagęszcza się w obszarach o dużych zmianach krzywizny;
-
dla krzywych wysokiego stopnia rośnie niestety nie tylko stopień wielomianów definiujących, ale także prawdopodobieństwo lokalnych i niezamierzonych ?szumów?, zwłaszcza wtedy, kiedy kształt wcześniej zdefiniowanej i poprawnej krzywej musi być nawet nieznacznie zmodyfikowany;
-
modyfikacje krzywej Béziera mają charakter globalny ? przesunięcie jednego punktu kontrolnego wpływa na kształt całej krzywej.

RYS. 1.
Rozwiązanie wydaje się oczywiste: rzeczywistą krzywą konstrukcyjną można podzielić na kilka (kilkanaście) segmentów, z których każdy jest krzywą Béziera. Nie można oczywiście zapomnieć o zachowania ciągłości pomiędzy takimi krzywymi cząstkowymi. Tu pojawia się jednak kolejne pytanie: jaki jest najniższy stopień krzywej Béziera, która zapewni spełnienie opisanych wcześniej wymagań konstrukcyjnych? Krzywe stopnia 1 mogą być zastosowane tylko jako modele linii prostej, a to zbyt mało, aby zdefiniować model dowolnej krzywej. Krzywe stopnia 2, czyli parabole, hiperbole lub elipsy także nie są odpowiednie, bo nie da się ich zastosować jako model krzywej z punktem przegięcia (RYS. 2), czyli w sytuacji, gdy krzywizna zmienia znak. Można sobie wyobrazić połączenie paraboli i elipsy w jedną krzywą, ale wtedy w punkcie wspólnym krzywizna krzywej wynikowej zmieniałaby się skokowo. A to oznacza, że maksymalna ciągłość takiej krzywej to G1, podczas gdy w większości nowoczesnych systemów wspomagających modelowanie powierzchniowe wymagana jest ciągłość typu G2.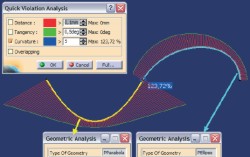
RYS. 2.
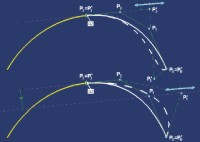
Więc może krzywa stopnia 3? Tak. Dwie krzywe Béziera stopnia 3 można ze sobą połączyć zachowując ciągłość typu G2 w ich punkcie wspólnym. Trzeba jednak zauważyć, że spełnienie kryterium ciągłości dwóch krzywych oznacza jednocześnie ograniczenie możliwości modyfikacji punktów kontrolnych krzywej (RYS. 3):
-
punkt P3 ma ustalone położenie ? jeśli dwie krzywe mają być ciągłe (ciągłość typu G0), to oczywiście nie można zmieniać położenia tego punktu;
-
punkt P2 wieloboku kontrolnego (najbliższy punktowi wspólnemu) można przesuwać TYLKO wzdłuż kierunku wyznaczonego przez punkty P2 i P3. Tylko, bo linia P2?P3 określa kierunek styczności do krzywej w jej punkcie końcowym P3 (czyli definiuje ciągłość typu G1), a dwie krzywe mają ciągłość typu G2 tylko wtedy, gdy są ciągłe według kryterium G1. Ponadto, aby zapewnić ciągłość G2, każda zmiana położenia punktu P2 na P2? ?wymusza? automatycznie zmianę położenia punktu P1 na P1?;
-
punkt P1 wieloboku kontrolnego (drugi z kolei licząc od punktu wspólnego krzywych) można przesuwać tylko po prostej równoległej do kierunku P2?P3.
-
punkt P0 może być dowolnie modyfikowany, chociaż zazwyczaj początek krzywej jest zdefiniowany przez warunki konstrukcyjne.
RYS. 3.
Jeśli można połączyć dwie krzywe Béziera stopnia d°=3 zachowując ciągłość typu G2 w ich punkcie wspólnym, to czy można skonstruować jedną krzywą, która zastąpi dwie krzywe Béziera? Rozważmy przykład krzywych cząstkowych (RYS. 4), których kształt jest określony przez dwa wieloboki kontrolne: P10?P11?P12?P13 i P20?P21?P22?P23:
-
jeśli te krzywe cząstkowe mają być ciągłe według kryterium G0, to punkt końcowy pierwszej z nich (P13) jest zgodny z punktem początkowym drugiej (P20) ? można powiedzieć, że wieloboki kontrolne tych krzywych ?trzymają się za ręce?. Krzywa wynikowa może być opisana przez 7 punktów kontrolnych;
-
jeśli te krzywe cząstkowe mają być ciągłe według kryterium G1, to oczywiście mają punkt wspólny (P20=P13) oraz zgodne kierunki styczności w tym punkcie (segmenty P13?P12 i P20?P21 leżą na tej samej linii prostej) ? można powiedzieć, że wieloboki kontrolne tych krzywych ?trzymają się za łokcie?. Krzywa wynikowa może być opisana przez 6 punktów kontrolnych (punkt P20=P13 można pominąć), a segment P2?P3 wieloboku kontrolnego krzywej wynikowej jest wspólny dla obu krzywych cząstkowych;
-
jeśli te krzywe cząstkowe mają być ciągłe według kryterium G2, to oczywiście mają punkt wspólny, zgodne kierunki styczności w tym punkcie, a położenie punktów P11 i P22 jest powiązane z położeniem odpowiednio punktów P12 i P21 w celu zapewnienia ciągłości zmian krzywizny krzywej wynikowej ? można powiedzieć, że wieloboki kontrolne tych krzywych ?trzymają się za ramiona i za łokcie?. Krzywa wynikowa może być opisana przez 5 punktów kontrolnych (punkt P2 powstaje na przecięciu kierunków P11?P12 i P21?P22), a segmenty P1?P2 i P2?P3 wieloboku kontrolnego krzywej wynikowej są wspólne dla obu krzywych cząstkowych.
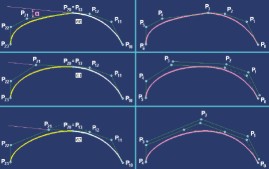
RYS. 4.
Wniosek jest oczywisty: Dwie krzywe Béziera stopnia d°=3 mogą być zastąpione jedną krzywą ?sklejoną?, która może mieć ciągłość G1 lub G2. Takie sklejane krzywe konstrukcyjne zbudowane z kilku krzywych Béziera nazywane są w teorii systemów CAD krzywymi typu Spline, (a właściwie B-Spline, gdzie B pochodzi od Basis Functions, które w poprzednim odcinku nazwałem ?wagami? punktów kontrolnych krzywej). Tu należałoby przypomnieć, że charakter zmian funkcji ?wagowych? zależy od stopnia krzywej, a wartości ?wag? przypisanych do każdego punktu wieloboku kontrolnego są jednoznacznie zdefiniowane dla dowolnego punktu krzywej, czyli dla dowolnej wartości parametru u. Reasumując można powiedzieć, że krzywe typu B-Spline mają następujące własności:
-
B-Spline, podobnie jak krzywa Béziera może mieć ciągłość typu G2;
-
liczba punktów wieloboku kontrolnego krzywej B-Spline jest mniejsza od sumy liczb punktów kontrolnych jej krzywych cząstkowych;
-
kształt krzywej typu B-Spline, podobnie jak krzywej Béziera, jest przybliżeniem rozkładu punktów kontrolnych, które przyciągają do siebie punkty krzywej w stopniu zdefiniowanym przez funkcje wagowe. W tym sensie krzywa typu B-Spline jest więc podobna do krzywej Béziera;
-
każdy z punktów kontrolnych Pi ma zdefiniowany zakres parametru u [ui, ui+1), w którym jego funkcja wagowa ma wartość większą od 0 ? dlatego B-Spline zapewnia lokalne modyfikacje krzywej.
O ile nie ma powodu dyskutować na temat pierwszych trzech własności, to ostatnia jest… co najmniej dyskusyjna. Zastanówmy się chwilę nad krzywą typu B-Spline zbudowaną z 3 krzywych Béziera stopnia 3 (RYS. 5), której kształt wynika z położenia 6 punktów kontrolnych. Punkty wspólne tych krzywych cząstkowych nazywamy węzłami krzywej sklejanej. Jeśli zmodyfikujemy położenie jednego z punktów kontrolnych drugiej z tych krzywych, opisanej wielobokiem P1?P2?P3?P4, to taka zmiana wpływa nie tylko na tą krzywą cząstkową, ale także na kształt pierwszej, trzeciej lub obu tych krzywych jednocześnie zależnie od tego, który punkt kontrolny jest modyfikowany. Na przykład jeśli zmienimy położenie punktu P2 lub P3, które kontrolują kształt wszystkich trzech segmentów krzywej pokazanej na rys. 5, to zmieni się kształt wszystkich trzech krzywych cząstkowych. Inaczej mówiąc lokalny charakter modyfikacji takiej krzywej nie zawsze oznacza zmianę kształtu jednej krzywej cząstkowej, bo dotyczy także przynajmniej jednej krzywej sąsiedniej. Trzeba jednak przyznać, że dla krzywej typu B-Spline, zbudowanej z 10 krzywych cząstkowych stopnia d°=3 nie są to zmiany globalne.

RYS. 5.
Byłoby idealnie gdyby możliwa była lokalna modyfikacja tylko jednej z krzywych cząstkowych krzywej sklejanej. Aby zapewnić jednocześnie ciągłość typu G2 i jak najbardziej lokalne możliwości modyfikacji, niektóre systemy CAD oferują algorytmy definiowania krzywych B-Spline zbudowanych z krzywych Béziera stopnia wyższego niż d°=3. Bo jeśli krzywa stopnia d°=3 ma ciągłość typu G2 w punkcie początkowym z inną krzywą, to w jej punkcie końcowym możliwe jest jedynie ustalenie ciągłości typu G0 (RYS. 6). Dopiero zwiększenie stopnia tej krzywej do d°=5 umożliwia zdefiniowanie ciągłości G2 na obu jej końcach ? odpowiednie położenie punktów P0, P1 i P2 wieloboku kontrolnego ustala ciągłość G2 w punkcie początkowym tej krzywej i analogicznie punktów P3, P4 i P5 ciągłość G2 w jej punkcie końcowym. Dlatego w przypadku ogólnym B-Spline może być zbudowana z krzywych Béziera stopnia d°=5. Przypomnę jednak, że zazwyczaj wystarczy d°=3, zwłaszcza wtedy, gdy modyfikacje krzywej sklejanej nie muszą być ograniczone do jednej krzywej cząstkowej lub wtedy, gdy krzywa sklejana może mieć ciągłość G1. Trzeba też pamiętać, że im wyższy jest stopień krzywych tym dłuższy jest czas obliczeń, a model geometryczny zajmuje więcej miejsca na dysku i w pamięci komputera.
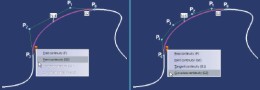
RYS. 6.
W oczekiwaniu na ciąg dalszy ?Elementarza…? zachęcam do analizy ciągłości krzywych B-Spline oraz modyfikacji jej wieloboku kontrolnego w celu uzyskania najlepszego rozkładu zmian krzywizny. A wszystko po to, aby mieć praktyczne podstawy do udzielenia odpowiedzi na pytanie: czy faktycznie B-Spline spełnia wszystkie oczekiwania konstruktora w zakresie definiowania i modyfikacji krzywych?
Autor: TEKST I RYSUNKI: ANDRZEJ WEŁYCZKO





